矩阵的行列式是一个可以从方形矩阵(方阵)计算出来的特别的数。
矩阵是数的排列:
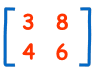
矩阵
(这矩阵有2行和2列)
这矩阵的行列式是(待会儿会解释计算方法):
3×6 − 8×4 = 18 − 32 = −14
用来干什么的?
行列式告诉我们矩阵的一些特性,这些特性对解线性方程组很有用,也可以帮我们找逆矩阵,并且在微积分及其他领域都很有用.
符号
行列式的符号是每边一条垂直线。
例子:
|A|代表矩阵 A的行列式
(和绝对值的符号一模一样。)
计算行列式
首先,矩阵一定要是方形矩阵(就是,行和列的数目相同)。计算方法其实很简单,只不过是基本的算术,如下:
2×2 矩阵
2×2 矩阵 (2行和2列):
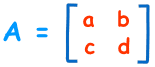
行列式是:
|A| = ad - bc
"A 的行列式等于 a 乘 d 减 b 乘 c"
|
把公式记住的窍门是想:十字乘法:
|
|
|
例子:
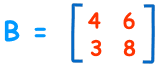
|
|B| |
= 4×8 - 6×3 |
|
|
= 32-18 |
|
|
= 14 |
3×3 矩阵
3×3 矩阵 (3行和3列):
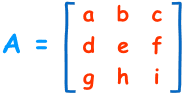
行列式是:
|A| = a(ei - fh) - b(di - fg) + c(dh - eg)
"A 的行列式等于。。。。。。"
乍看很复杂,但这是有规律的:
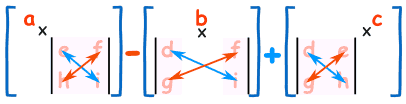
求 3×3 矩阵的行列式:
- 把 a 乘以不在 a 的行或列上的 2×2
矩阵的行列式。
- 以 b 和 c 也做相同的计算
- 把结果加在一起,不过 b 前面有个负号!
公式是(记着两边的垂直线 || 代表 "的行列式"):
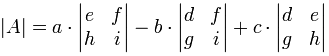
"A 的行列式等于 a 乘 。。。。。。的行列式。。。。。。"
例子:
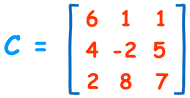
|
|C| |
= 6×(-2×7 - 5×8) - 1×(4×7 -
5×2) + 1×(4×8 - -2×2) |
|
|
= 6×(-54) - 1×(18) + 1×(36) |
|
|
= -306 |
4×4 和更大的矩阵
同一规律也适用于 4×4 矩阵:
- 加:a 乘以 不在 a 的行或列 的矩阵 的行列式,
- 减:b 乘以 不在 b 的行或列 的矩阵 的行列式,
- 加:c 乘以 不在 c 的行或列 的矩阵 的行列式,
- 减:d 乘以 不在 d 的行或列 的矩阵 的行列式,

公式是:
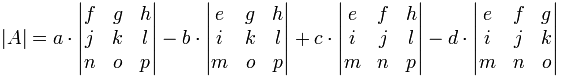
留意 + - + - 的规律(+a 。。。-b 。。。+c 。。。-d 。。。)。 这很重要,要牢记。
同样的规律也适用于5×5 和更大的矩阵,但通常最好是用矩阵计算器来处理大的矩阵!
并非唯一的方法
这个计算放法叫 "拉普拉斯展开"。。。。。。我喜欢它,因为规律容易记。但亦有其他的计算方法(我只想你知道)。
总结
- 2×2 矩阵的行列式是 ad - bc
- 3×3 矩阵,把 a 乘以 不在 a 的行或列 的矩阵 的行列式。b 和 c 也做同样的计算,但 b 前面有个负号!
- 更大的矩阵也跟随相同的规律: 把 a 乘以 不在 a 的行或列 的矩阵 的行列式;第一行的每个元素都这样做;然后把结果跟随 + - + - 的规律加/减起来。